Mesh Embedding Module
Function Purpose
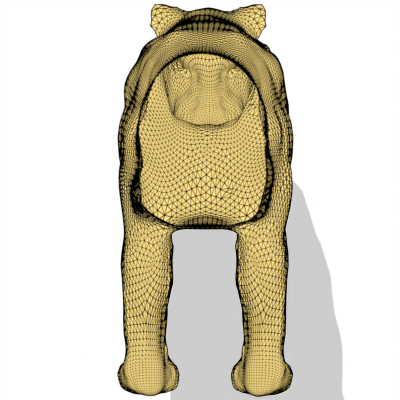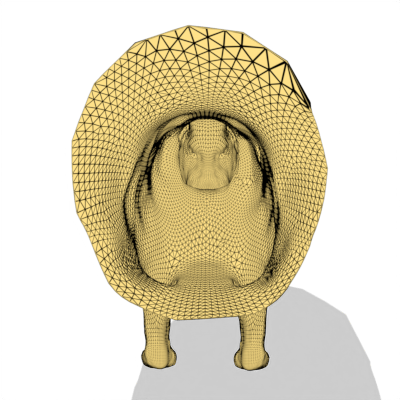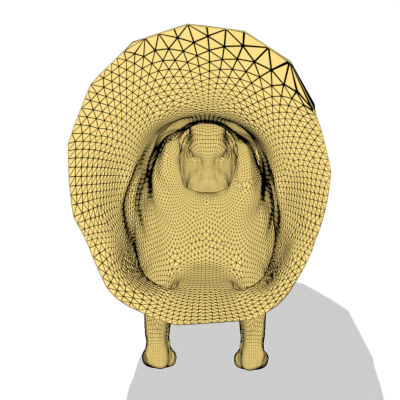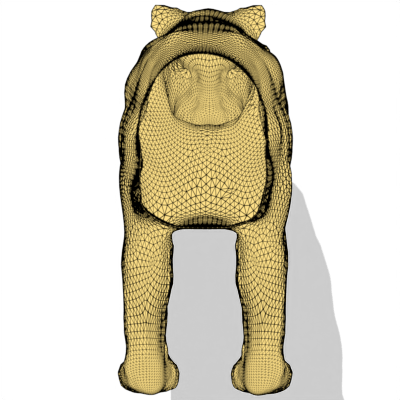
Implements Tutte's embedding algorithm to parameterize 3D open meshes with a single boundary loop onto a 2D convex polygon.
Function Signature
MeshTypes::Mesh2D result_mesh = MeshEmbedding::TutteEmbedding::Parameterize(
const MeshTypes::Mesh3D& mesh,
const std::vector<std::vector<size_t>>& boundary_chains,
const size_t weight_type = 1,
const size_t check_interval = 100,
const size_t max_iterations = 100000000
);Input Parameters
mesh(MeshTypes::Mesh3D structure)-
vertices: Vector of 3D coordinates (v1, v2, ..., vN)faces: Vector of triangular faces (t1, t2, ..., tM)
boundary_chains(2D vector<size_t>)-
Boundary vertex sequences:
- Format: {{v11,...,v1N1}, {v21,...,v2N2},..., {vL1,...,vLNL}}
- Boundary continuity: viNi = v(i % L + 1)1, i = 1, 2,..., L
weight_type(size_t)-
Weighting scheme selection:
- 0: Uniform Laplace weights: wij = 1
- 1: Mean value coordinates (default):
wij = [tan(α/2) + tan(β/2)] / ||vi - vj||where α and β are angles adjacent to edge (i,j)
check_interval(size_t)- Injectivity verification frequency (default: 100 iterations)
max_iterations(size_t)- Maximum solver iterations (default: 108)
Output
result_mesh (MeshTypes::Mesh2D structure)vertices: Vector of 2D coordinates (v'1, v'2, ..., v'N)faces: Vector of triangular faces (t1, t2, ..., tM)
Example
main.cpp
Critical Notes
- Input Mesh Requirements:
- Must be a 3D open manifold
- Must have genus-0 topology
- Must maintain triangular mesh structure
- Orientation Consistency:
Ensure consistent triangle orientations using:
MeshEmbedding::UnifyTriangleOrientations(MeshTypes::Mesh3D& mesh);
prior to parameterization - Numerical Precision:
Double-precision computation required for guaranteed injective mapping
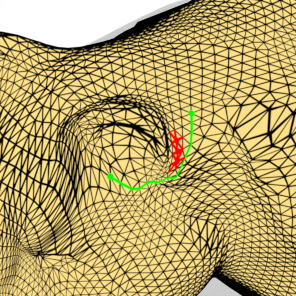
- Boundary Ear Triangle Constraint:
Vertices shared by only one triangle must appear exclusively at boundary chain endpoints to prevent degeneration